Two blocks of equal mass that are connected by a rigid bar of length l move without friction along a given path. The attraction of the earth acts along the negative y-axis. Find the equation for the generalized coordinate α.
First, let's try to get the relation between the Cartesian coordinates and our generalized coordinate:
To get the Lagrangian, we need the potential and kinetic energies.
And the potential:
Now we can write the Lagrangian as L = T - V:
And the Lagrange equation remains as:
And finally, we get the equation of the system based on the generalized coordinate α:
We can solve the previous differential equation knowing that α is a time dependent variable, or let the equation as this.
As we can see, the Lagrangian help us getting the equation of the system with simple methods. Solving this problem with the Newtonian mechanics could lead to more complicated calculus.
We can solve the previous differential equation knowing that α is a time dependent variable, or let the equation as this.
As we can see, the Lagrangian help us getting the equation of the system with simple methods. Solving this problem with the Newtonian mechanics could lead to more complicated calculus.


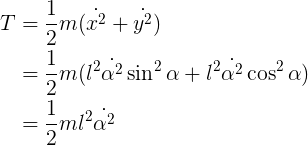


No comments:
Post a Comment