Joseph-Louis Lagrange (1736-1813) was a mathematician, physicist and astronomer which made important contributions to analysis, number theory and classical and celestial mechanics. Mécanique analytique (1788) was his treatise where he first introduced the analytical mechanics. He first invented the Lagrangian function which verify the Lagrange equations. The Lagrangian is a reformulation of the classical mechanics, which simplify the calculations.
But before going directly to the Lagrange equations, let's start with the virtual displacement. Consider a system made of a pipe which rotate on a fixed at one end, and where some particles come from the fixed end of the pipe and get out from the pipe by the other end. The real displacement of the particles will be the rotating displacement plus the centrifugal force. This displacement, is commonly denoted as dr. The virtual displacement is the displacement if all the forces and constraints acting on the system do not change. This is, if for an infinitesimal amount of time, the pipe will not rotate. Then, the particle will only have the centrifugal force, which made only the radius vector. This displacement is commonly denoted as δr.
Let's now return to the Lagrange equations. The second law of Newton says that the force on a particle is:
Let's now return to the Lagrange equations. The second law of Newton says that the force on a particle is:
If we decompose the force into the applied force Fa, and the constraints force f, the Newton's law becomes:
Considering a system in equilibrium, the total work of the system will be zero. As the work is the force multiplied by the displacement, the virtual work will be also zero:
In the case of a rigid body, the multiplication of a contraint force of a single particle of the rigid body with its virtual displacement will be zero; as the virtual displacement will be perpendicular to the constraint force. Imagine a particle on a pendulum, the contraint force will from the particle to the fixed point of the string, and the virtual displacement will be tangent to the circle made by the rotating string. This leads the previous equation to the principle of virtual work:
We also know that the force is the derivative of the momentum:
Substituting this on the principle of virtual work, we have the D'Alembert principle:
The D'Alembert principle states the dynamic equilibrium of a system of particle.
Let's now consider a holonomic contraint ri(q1, q2, ..., qN, t) = 0. A holonomic constraint is all the equations which restrict the movement of our particles system where the time is involved in those equations. This means that each coordinate ri can be defined by some equations where generalized coordinates qi are defined.
Then we can define the velocity as:
Then we can define the velocity as:
And the virtual displacement as:
Note that the time does not appear here, since the virtual displacement, by definition, considers only displacements of the coordinates. Going back again to our equation of the virtual work, we can use generalized coordinates:
Here, Qk is called the generalized force as it depends on the generalized coordinates. Note that q does not necessarily have the dimension of force as Q does not necessarily have the dimension of force, but the product of both must have the dimension of work (it might be the torque for Q and the angle for q).
Let's go back to the D'Alembert principle and use the generalized coordinates for the momentum:
Consider now the following relation:
For the last term, we can interchange the differentiation variable to obtain the velocity:
Substituting this result in the previous equation:
From the above equation obtained of the velocity, we know that this equality is true:
Substituting all this, we get:
Reordering this equation:
In the previous equation, we can now see the term of the kinetic energy T:
Making the adequate substitutions in the D'Alembert principle with the generalized coordinates:
Let's now use a potential function. Consider the forces are derivable from a scalar potential function V as follows:
By definition of the generalized force, we can link the potential function as follows:
Which lead to the final equation:
I've also included V in the first term of the equation, which does not affect the result as the potential field does not depend on the generalized velocities. This lead to the Lagrange's equation with the substitution of L = T - V which is known as the Lagrangian.
But what's the Lagrangian and the Lagrange's equation for? From the values of the kinetic and the potential energies, we can easily get the equation of movement of a system of particles. With the Lagrange's equation we'll have a system of equations (one per generalized coordinate) which is only composed by the kinetic and potential energy (which are quite easily to obtain in most of the cases).
To see this, let's solve an exercice.


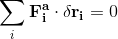

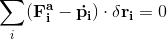
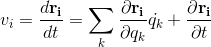
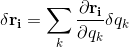




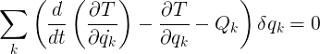


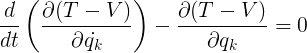
No comments:
Post a Comment