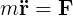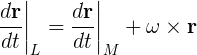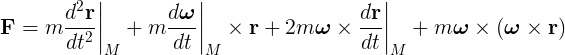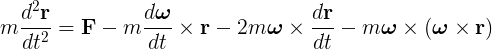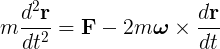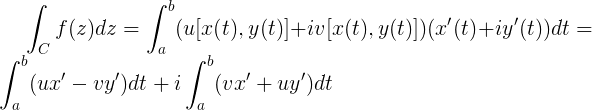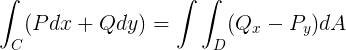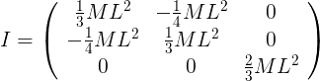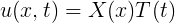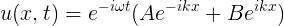Classical Mechanics - Coriolis Acceleration

The Coriolis acceleration is a phenomena which appears when the reference system where the coordinates are taken is under a rotating acceleration. If the reference system isn't affected by a rotating acceleration, it's an inertial system, otherwise (in this case) it's a non-inertial system. Let's try to see this starting with the Newton's laws:

As I said, our reference system is under a rotating acceleration, so the velocity vector must be adapted (I will use the subscript L to name the "Laboratory system" which is the inertial system, and the subscript M to name the "Moving system" which is the non-inertial system):

As we see, the angular velocity of the moving system must be added to the linear velocity of the moving system. Let's derive the previous equation to obtain the acceleration. To do so, I will first introduce the operator D:

And now the derivative can be obtained easily:

Substituting the D operator:

The first term of the result is the linear acceleration. We can see easily that if it were no angular velocity, this will be the unique remaining term; which means that the acceleration has the same value independently of the reference system (in an inertial system). The second term is angular acceleration. The third is the Coriolis acceleration. And the last term is the centripetal acceleration.

Now we can rewrite the Newton's law for a non-inertial system just multiplying the previous equation by the mass:

If we leave the main force over the particle in the left hand of the equation (and omitting the M subscript):

Let's do an exercice to apply the obtained equation.

A river of width D flows on the northern hemisphere at the geographical latitude φ toward the north with a flow velocity v₀. By which amount is the right bank higher than the left one?

First of all, let's examine each term of the equation for our case. The force vector will represent the gravitational force. The angular acceleration is zero as our angular velocity is the earth rotation which is constant. And the centripetal acceleration can be omitted, as the r vector is small compared with the radius of the earth (which is present the the gravitational force). This leads us to the simplified equation:

Let's now define the force vector, the angular velocity and the linear velocity in the non-inertial system. I will consider the orthonormal basis u'_x (from north to south coordinate), u'_y (from west to east coordinate) and u'_z (the up-down coordinate) as the basis on the non-inertial system.

Now we can rewrite the motion of the river equation:

Here, we can appreciate two forces, one downward the earth, and the other to the east. This make a vector which pulls the surface of the water in this direction. With the modulus of this force, and one of its component, we can obtain the angle of this force. This angle, with the width of the river gives us the difference of high between one side to the other of the river.

Complex Analysis - Cauchy Goursat Theorem

When talking about integrals in the complex analysis, the Cauchy Integral Formula is very important. Rather than putting the formula here, and then explain it, I'll try to reach to the formula with the help of other theorems, which will give more explanation about its importance.

First of all, let's see an integral on the complex plane:

This is an integral over a closed contour (counterclockwise). I assume that f is analytic at each point interior to and on C. If we define f(z) and z(t) as a real and imaginary parts:

we can now substitute it on the integral and separate the real part and the imaginary part:

We know that ux' is udx which is the real part of a function derived by the real component, and vy' is vdy which is the imaginary part of a function derived by the imaginary component, and so on. This remains as:

Let's now apply the Green's Theorem to the preceding integral:

From an integral over a closed contour, we reach to a double integral over the domain interior of the contour with partial derivatives. Applying this to our case:

As we have partial derivatives, we can apply the Cauchy-Riemann equations u_x = v_y and u_y = -v_x.

As we see, the Cauchy-Goursat Theorem tells us that an integral over a positive closed contour of a function which is analytic on the contour and inside is zero.

Classical Mechanics - The Tensor of Inertia

The tensor of inertia is a tensor very used to describe the rigid body motion. But what's a tensor? And what's the inertia? The inertia is basically the "force" a rigid body has to avoid accelerations. If a rigid body has a high inertia, it's difficult to move it (or to stop it if is in movement); and if a rigid body has a low inertia, you can easily move it or stop it. Basically, the inertia is represented as:

It's the integral over the mass of the rigid body of the position squared. Analyzing the definition giving at the beginning, we can see that for two bodies of the same size, the heaviest have a higher inertia as it's more difficult to move it or stop it.

Ok, but what's the tensor of inertia? And what's a tensor? As said in our definition of inertia, this is related with the movement, as the angular velocity. Thus, the angular momentum also defines the structure of a body, the difficulty to move or stop it. All this three magnitudes are related as follows:

The equation continues verify our definition of the inertia, as if a body with a high inertia with a high angular velocity has a higher force (angular momentum) than the same body with lower angular velocity.

And the definition of the tensor? Here we go. Let the body move in three dimensions, have an angular velocity on the three axis. This will lead to three angular momentum, one per axis. This means that the inertia multiplied by the angular velocity (which has three components) is equal to the angular momentum (which also has three components). So, what type of structure can allow this vector multiplication? A matrix. A tensor is a matrix, is a vector with an addition dimension. As the vector has an additional dimension over a scalar value, a matrix has an additional dimension over a vector. It's quite difficult to imagine a tensor in the real life but let's try it. When you throw an object in the air, rotating it only in one axis, you will see as it turns in other axis. You give to the object an angular velocity with only one component, but as the object turns in the three axis when it's in the air, this means that the inertia of the object absorbs the movement of a single dimension and reflect it in three dimensions. It's quite hard to imagine it, but try with your mobile phone, you'll see as it rotates in more than one axis when you throw it (and util it crashes on the ground).

Ok, let's now build a tensor of inertia. Here is how it looks like:

First of all, the tensor of inertia is symmetric, this means that I_xy = I_yx. But how to calculate all those values? With the formula given at the beginning, the formula of the inertia. We only have to substitute r by the adequate coordinate of the matrix. Let's see it:

But why are there negative signs? This comes from the definition of the angular momentum.

Well, I think it's time for an example to complete the definition. Let's try to obtain the tensor of inertia of a square covered with mass. The square has only two dimensions (let's suppose the square in the X-Y plane), this means that all the components of the tensor inertia which are multiplied by the Z component are zero. Let's determine the others

With those components, we've got the tensor of inertia:

Differential Equations - Separation of Variables

When you have a differential equation (or a system of differential equations) which depends on several independent variables, you can't use the ordinary methods to solve the equation (or the system of equations). 

The separation of variables method can solve some differential equations (from now, the examples will be based on a single differential equation, but the method can be extended to a system of differential equations) assuming to be composed of several equations (one per independent variable) and satisfying some boundary values. This way, as we have separated differential equations with a single independent variable, we can use the known methods to solve it. But be aware that the boundary values can lead to unsolvable equations or equations with infinite solutions.

Let's suppose a differential equation with two independent variables which can be separated as following:

Where X(x) depends only on the independent variable x, and T(t) depends only on the independent variable t. Let's use a particular case, the wave equation in one space dimension.

Now, I'll obtain the derivative of the function u of the first example from each variable.

Substituting this results in the heat equation, we obtain:

This way, we have in the left hand only the independent variable t, and in the right hand the independent variable x. As they are independent variable from each other (a variation on x does not affect the value of t), we can assume that the result of the last fraction is constant. As variations on x will only affect the right hand, so the left hand must remain constant, the same for variation on t.

Where λ is a constant. The previous result is composed of two differential equations with a single independent variable each one. So, this is a system which can be easily solved with known methods. Let's proceed.

Now, depending on the value of λ and the boundary values, the solution can be quite different: possible, impossible or infinite. Let's examine the different cases depending on the value of λ (I'll only use the X(x) function):

• λ greater than 0. In this case, the solution of the differential equations is as follows:

Let's examine the values of the constants. For x = 0 and x = L we have u = 0. This lead to:

The resulting equation is only valid if λ is less than 0 (we assumed it is greater than zero at the beginning) or C₁ = 0 which leads to C₂ = 0 too. This means that there is only a trivial solution when λ is greater than zero.

• λ equal to 0. This case is quite more simple. The solution of both equations are:

But applying the boundary values, we quickly reach to a trivial solution too.

• λ less than 0. Here, we must lead with imaginary results, which have the following result in a differential equation:

As we supposed λ to be negative, the square root remains with positive values inside. Let's now apply the boundary values:

Here, we have a non trivial solution when λ = -(n π / L)² for n = 1, 2, 3... Having the value of λ, we can quickly obtain the value of T(t):

Giving a solution of the partial differential equation as:

As each of the u_n are a solution of the wave equation, a linear combination of all the u_n is also a solution of the wave equation:

The solution above is not the known as the wave equation, but with some basic mathematical modifications, we easily come to the famous wave equation:

C - Fractals

In the following article, I'm gonna show how to build an application to draw the Sierpinski Triangle (https://en.wikipedia.org/wiki/Sierpinski_triangle). The Sierpinski Triangle is a fractal figure which represent a triangle, and inner triangles leaving always the central one intact. This is a great exercice to do in C, as it trains the loops and pointers.

The application must generate a Sierpinski triangle of a given number of steps (it will be an input argument of the main application) and plot the result into a PNG file with gnuplot. As every programming application, there isn't a single way to build the application. Here, I'm going to show the solution, and how I developed the solution. The way I do, is going from the generic to the specific. First of all, write the main.c file calling both the SierpinskiGenerator and the plot. As those two functions are not yet defined, I don't know which parameters they need, so, I'll assume what they should need and correct it later (I almost know which parameters they need, as I spend some hours doing the application, but in a usual workflow, you don't know). The SierpinskiGenerator should need the size of the main triangle, and the number of iterations. I let the SierpinskiGenerator work already with pixels, this way I won't need to convert from some arbitrary convention to pixels when plotting the result. But usually, you should have a abstract generator and some translators, this way your generator will give you some results, and you can plot it with a translator to pixels, to write it to a CSV file with a CSV translator... But for the current example, it will reduce complexity if I work in all the application with pixels.

The plot function will need the data of the generated triangles, and the amount of triangles. I assume that in the triangles there is already the pixels information. Here is the code of main.c:

From lines 10 to 12 I've made a validation allowing the application to run only if the number of iteration is specified, otherwise, nothing will happen (only a warning/error message will be shown).

Let's go now with Sierpinski generator. First off all, as seen in the main.c, there is a Triangle data type. This is a defined structure in C. A triangle is composed of 3 corners, and each corner is composed of two coordinates (X and Y). Instead of handling a list of float with all those values, I've grouped all of them in two structures: Point and Triangle:

I've stored the structures in the sierpinski.h file as this is the main entry point of those structures. Importing the sierpinski.h file, I can use the Triangle and Point structures everywhere.

For the Sierpinski generator, I've made two implementation, the first one with for-loops (multiple levels), and the second one with recursion. What's the recursion? When a method call itself. This is useful with multiple mathematical applications and in particular with fractals. 

Let's start with the easiest, the for-loops. I have to iterate into a first for-loop the number of steps given by the user. Inside this for-loop, I have to iterate over all the existing triangles and generate inner triangles. I create two methods: one to generate a single inner triangle (the central one), and a second to obtain all the triangles except the central one (by elimination). Here are those two methods:

As you can see, the structures, can be used with the sizeof method too (which is very useful to allocate the memory). 

And here is the main method, which build our complete Sierpinski triangle:

The first implementation has 3 for-loops (line 25, 26 and 29), which means that when the steps of the Sierpinski triangle increase, this could lead to an important time consuming for the machine. Let's examine the code. First allocate enough memory for all the triangles. Then initialize the first triangle with the given size. And finally, the loops. The first loop will iterate over the number of steps of our fractal. The second will iterate over the existing triangles, and the third will prepare the data for the next fractal iteration saving the triangle data into a separated variable. This is also done in line 35 with the memcpy method which allow you to copy the data from a pointer to another pointer.

Go now with the second implementation. I haven't made a lot of changes inside the methods, to maintain the readability of the code.

The first method is similar to the first implementation, and the second method is the one used in recursion (you can see that the generate_sierpinski_triangle_recursively is called at line 71). This allow us to hide a for-loop. I said hide, as the loop is still there, it's the recursion. The initial condition is the iteration value; the final condition is at line 70; and the statement for each step is at line 71 (--iterations).

Which implementation is the best? It depends. The behavior is quite similar, there are some differences at memory consumption and CPU usage (the first allocate a lot of memory at the beginning, but the second is constantly allocating memory). If there are a lot of for-loops, the second implementation is better for readability (all is split into smaller methods), but you have to do it carefully as the exit condition is not as explicit as the for-loop.

And finally the graph generation. gnuplot was used to plot the graph. Each triangle will be plotted with lines. Here is the code of plot.c:

As said at the beginning, this is not the only (and best) solution of the problem, but I tried to do it in a way which could easily be understood.