When talking about integrals in the complex analysis, the Cauchy Integral Formula is very important. Rather than putting the formula here, and then explain it, I'll try to reach to the formula with the help of other theorems, which will give more explanation about its importance.
First of all, let's see an integral on the complex plane:
This is an integral over a closed contour (counterclockwise). I assume that f is analytic at each point interior to and on C. If we define f(z) and z(t) as a real and imaginary parts:
we can now substitute it on the integral and separate the real part and the imaginary part:
We know that ux' is udx which is the real part of a function derived by the real component, and vy' is vdy which is the imaginary part of a function derived by the imaginary component, and so on. This remains as:
Let's now apply the Green's Theorem to the preceding integral:
From an integral over a closed contour, we reach to a double integral over the domain interior of the contour with partial derivatives. Applying this to our case:
As we have partial derivatives, we can apply the Cauchy-Riemann equations ux = vy and uy = -vx.
As we see, the Cauchy-Goursat Theorem tells us that an integral over a positive closed contour of a function which is analytic on the contour and inside is zero.

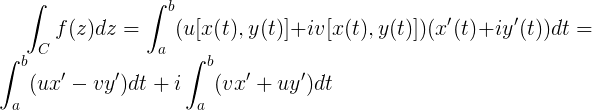

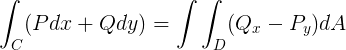


No comments:
Post a Comment