When you have a differential equation (or a system of differential equations) which depends on several independent variables, you can't use the ordinary methods to solve the equation (or the system of equations).
The separation of variables method can solve some differential equations (from now, the examples will be based on a single differential equation, but the method can be extended to a system of differential equations) assuming to be composed of several equations (one per independent variable) and satisfying some boundary values. This way, as we have separated differential equations with a single independent variable, we can use the known methods to solve it. But be aware that the boundary values can lead to unsolvable equations or equations with infinite solutions.
Let's suppose a differential equation with two independent variables which can be separated as following:
Where X(x) depends only on the independent variable x, and T(t) depends only on the independent variable t. Let's use a particular case, the wave equation in one space dimension.
Now, I'll obtain the derivative of the function u of the first example from each variable.
Substituting this results in the heat equation, we obtain:
This way, we have in the left hand only the independent variable t, and in the right hand the independent variable x. As they are independent variable from each other (a variation on x does not affect the value of t), we can assume that the result of the last fraction is constant. As variations on x will only affect the right hand, so the left hand must remain constant, the same for variation on t.
Where λ is a constant. The previous result is composed of two differential equations with a single independent variable each one. So, this is a system which can be easily solved with known methods. Let's proceed.
Now, depending on the value of λ and the boundary values, the solution can be quite different: possible, impossible or infinite. Let's examine the different cases depending on the value of λ (I'll only use the X(x) function):
Let's examine the values of the constants. For x = 0 and x = L we have u = 0. This lead to:
- λ greater than 0. In this case, the solution of the differential equations is as follows:
Let's examine the values of the constants. For x = 0 and x = L we have u = 0. This lead to:
The resulting equation is only valid if λ is less than 0 (we assumed it is greater than zero at the beginning) or C1 = 0 which leads to C2 = 0 too. This means that there is only a trivial solution when λ is greater than zero.
- λ equal to 0. This case is quite more simple. The solution of both equations are:
But applying the boundary values, we quickly reach to a trivial solution too.
- λ less than 0. Here, we must lead with imaginary results, which have the following result in a differential equation:
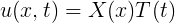




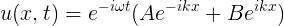
No comments:
Post a Comment