The tensor of inertia is a tensor very used to describe the rigid body motion. But what's a tensor? And what's the inertia? The inertia is basically the "force" a rigid body has to avoid accelerations. If a rigid body has a high inertia, it's difficult to move it (or to stop it if is in movement); and if a rigid body has a low inertia, you can easily move it or stop it. Basically, the inertia is represented as:
It's the integral over the mass of the rigid body of the position squared. Analyzing the definition giving at the beginning, we can see that for two bodies of the same size, the heaviest have a higher inertia as it's more difficult to move it or stop it.
Ok, but what's the tensor of inertia? And what's a tensor? As said in our definition of inertia, this is related with the movement, as the angular velocity. Thus, the angular momentum also defines the structure of a body, the difficulty to move or stop it. All this three magnitudes are related as follows:
The equation continues verify our definition of the inertia, as if a body with a high inertia with a high angular velocity has a higher force (angular momentum) than the same body with lower angular velocity.
And the definition of the tensor? Here we go. Let the body move in three dimensions, have an angular velocity on the three axis. This will lead to three angular momentum, one per axis. This means that the inertia multiplied by the angular velocity (which has three components) is equal to the angular momentum (which also has three components). So, what type of structure can allow this vector multiplication? A matrix. A tensor is a matrix, is a vector with an addition dimension. As the vector has an additional dimension over a scalar value, a matrix has an additional dimension over a vector. It's quite difficult to imagine a tensor in the real life but let's try it. When you throw an object in the air, rotating it only in one axis, you will see as it turns in other axis. You give to the object an angular velocity with only one component, but as the object turns in the three axis when it's in the air, this means that the inertia of the object absorbs the movement of a single dimension and reflect it in three dimensions. It's quite hard to imagine it, but try with your mobile phone, you'll see as it rotates in more than one axis when you throw it (and util it crashes on the ground).
Ok, let's now build a tensor of inertia. Here is how it looks like:
First of all, the tensor of inertia is symmetric, this means that Ixy = Iyx. But how to calculate all those values? With the formula given at the beginning, the formula of the inertia. We only have to substitute r by the adequate coordinate of the matrix. Let's see it:
But why are there negative signs? This comes from the definition of the angular momentum.
Well, I think it's time for an example to complete the definition. Let's try to obtain the tensor of inertia of a square covered with mass. The square has only two dimensions (let's suppose the square in the X-Y plane), this means that all the components of the tensor inertia which are multiplied by the Z component are zero. Let's determine the others





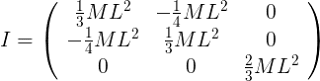
No comments:
Post a Comment