The Coriolis acceleration is a phenomena which appears when the reference system where the coordinates are taken is under a rotating acceleration. If the reference system isn't affected by a rotating acceleration, it's an inertial system, otherwise (in this case) it's a non-inertial system. Let's try to see this starting with the Newton's laws:
As I said, our reference system is under a rotating acceleration, so the velocity vector must be adapted (I will use the subscript L to name the "Laboratory system" which is the inertial system, and the subscript M to name the "Moving system" which is the non-inertial system):
As we see, the angular velocity of the moving system must be added to the linear velocity of the moving system. Let's derive the previous equation to obtain the acceleration. To do so, I will first introduce the operator D:
And now the derivative can be obtained easily:
Substituting the D operator:
The first term of the result is the linear acceleration. We can see easily that if it were no angular velocity, this will be the unique remaining term; which means that the acceleration has the same value independently of the reference system (in an inertial system). The second term is angular acceleration. The third is the Coriolis acceleration. And the last term is the centripetal acceleration.
Now we can rewrite the Newton's law for a non-inertial system just multiplying the previous equation by the mass:
If we leave the main force over the particle in the left hand of the equation (and omitting the M subscript):
Let's do an exercice to apply the obtained equation.
A river of width D flows on the northern hemisphere at the geographical latitude φ toward the north with a flow velocity v0. By which amount is the right bank higher than the left one?
Let's now define the force vector, the angular velocity and the linear velocity in the non-inertial system. I will consider the orthonormal basis u'x (from north to south coordinate), u'y (from west to east coordinate) and u'z (the up-down coordinate) as the basis on the non-inertial system.
Now we can rewrite the motion of the river equation:
Here, we can appreciate two forces, one downward the earth, and the other to the east. This make a vector which pulls the surface of the water in this direction. With the modulus of this force, and one of its component, we can obtain the angle of this force. This angle, with the width of the river gives us the difference of high between one side to the other of the river.
Now we can rewrite the motion of the river equation:
Here, we can appreciate two forces, one downward the earth, and the other to the east. This make a vector which pulls the surface of the water in this direction. With the modulus of this force, and one of its component, we can obtain the angle of this force. This angle, with the width of the river gives us the difference of high between one side to the other of the river.
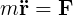
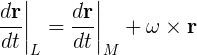





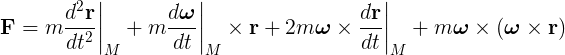
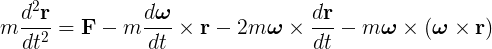

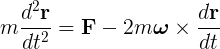




No comments:
Post a Comment