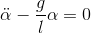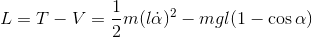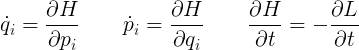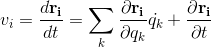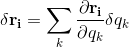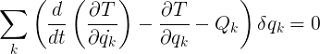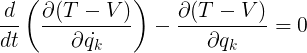Quantum Mechanics - Planck's constant

The black body radiation

The quantum mechanics started by the black body radiation problem. At the end of the XIX century, physicists tried to explain the spectrum of frequencies originated by the thermal energy of a body. The concept was idealized to the black body, a body which absorbs all the energy received and doesn't reflect it; this allow us to know that all the radiation emitted by the black body comes from the thermal energy (and not by any other surrounding body which radiation is reflected in the black body). A black body is an hypothetical object, but which can be simulated by a rigid box with a cavity and a small hole where the internal radiation can escape. The box must in equilibrium with its environment. The radiation will start into the box, and escape from the some hole. As the hole is small compared with the box, we can consider the escaped radiation to be insignificant with the rest, which made the radiation still constant inside the box.

The spectrum which offers the black body has a maximum intensity at some frequency which is proportional to the temperature. But as you increase the temperature, the intensity decrease. Lord Rayleigh and Sir James Jeans imagined the radiation originated by oscillators (as the electrons rotating around the atomic nucleus) in the internal walls of the black body. By applying the classical mechanics, those oscillators will increase their energy as the temperature increase (E = kT/2, where E is the thermal energy, k the Boltzmann constant and T the temperature). Applying this energy to classical oscillators (E = kA²/2 = kx²/2 + mv²/2)  we already see that, as the amplitude of the oscillators won't change, the velocity must; this leads to a higher frequency. The relation of the temperature and the frequency is exponential. This leads to the ultraviolet catastrophe. This means that higher the temperature is, higher the intensity at higher frequency is, and this is not true as the sun radiation should radiate us with high intensive ultraviolet rays, but doesn't.

So, another explanation should be giving to the black body problem. And Max Planck comes with the clue.

Hypothesis of quanta

Max Planck started from the Boltzmann work which defines the entropy. He consider the entropy as an absolute value, as when you divide a gas in smaller parts until you have a single atom, the minimum equilibrium state of this single atom will define the initial state of the entropy. Adding more and more atoms, you increase the entropy by discrete quantities (as you introduce a discrete number of atoms). This was called the hypothesis of quanta.

Applying this to the oscillators introduced by Rayleigh and Jeans, we can first obtain the state of a microscopic oscillator by its coordinates, which are two: the moment, and the rate at which it varies. The region of this state plane defined by those two coordinates, will be constant and equals to h (the Planck's constant) which has the dimension of erg sec.

How does this affect the oscillators? Knowing that the amplitude of the oscillators will remain constant, and the product of the moment and its derivative too, there will be a region in the plane phase were the oscillator will be moving, which draws an ellipsis (with the moment in a semi-axis and its derivative in the other semi-axis). This lead to a energy state as E = nhv, where h is the Planck's constant, v is the frequency of the oscillator, and n is a positive integer which defines the region in the plane phase of the oscillator.

Coming back to the entropy, we must now connect this energy with the entropy. The second principle of the thermodynamics give it to us as dS = dE/T, and leads to:

At this point, we clearly see that for a given temperature, the energy don't tends to infinite for higher frequencies, which solve the ultraviolet catastrophe.

Planck postulate

From the energy state obtained, Planck enunciates its postulate as each physical entity with a single mechanical degree of freedom where its coordinates origins a simple harmonic motion can only have discrete values of energy represented by E = nhv (where n is a positive integer). 

This quickly comes to the definition of the atomic structure, and helps Bohr to enunciate its atomic model. The Planck's constant was the entry point to the quantum mechanics, which forbids the energy to be continuous but discrete. This also helps the understanding of the wave-particle duality of the light.

Classical Mechanic - Hamiltonian exercise

Let's try to solve the pendulum equation with the Newton's, Lagrange's and Hamilton's mechanics.

Newton's Mechanics

The K vector shows the direction of the movement of the pendulum. It can be defined as |K| = mgsinα. Consider the displacement of the mass at the end of the pendulum as x. So the vector K remains as:

We know the value of the displacement x and its second derivative as:

If we substitute those values in the precedent equation, and making the approximation of the sinus for small displacements of we get:

Solving this differential equation of order 2, we get:

Lagrange's Mechanics

Here, we must first find the kinetic and potential energies:

With those energies, we can obtain the Lagrangian:

Now we can apply the Lagrange's equation to obtain the motion of the pendulum:

This is the same differential equation as the one get with the Newtonian mechanics.

Hamilton's Mechanics

We start from the Lagrangian, and the generalized momentum:

Now, with the value of the generalized momentum, we can substitute the derivative of α from the Lagrangian and get the Hamiltonian:

If, now, we apply the Hamilton's equations:

Substituting the values of the generalized momentum, we reach to the same differential equation as in the two other cases; with the same final result.

Conclusion

As you've see, the three methods hopefully gave the same result, which confirm that they are a reformulation of the same mechanics. The Newton's mechanics is more simplistic, and for problems with more constraints, you must deal with a system of several equations.

The Lagrangian's mechanics reduce the number of equations to the number of constraints. This is the method with less equations to solve, but you must deal with almost a differential equation of order two.

And the Hamiltonian's mechanics have twice the number of equations than the Lagrangian, but you with easier calculus, as the Hamilton equations does have second degree derivatives.

Classical Mechanics - Hamiltonian

Sir William Rowan Hamilton (1805-1865) was the creator of the quaternions, but also known for its contributions in the Newtonian mechanics (as he reformulated it in the Hamiltonian mechanics) and in the Quantum mechanics.

Why do we need another reformulation of the Newtonian mechanics having the Lagrangian? Let's examine the Lagrangian:

As we can see, the Lagrangian depends on the kinetic energy, which has the velocity as its component. The velocity is a derivative of the position. And in the first term of the Lagrange's equation, the Lagrangian is derived by the time, this means that we'll have the position derived twice by the time, which lead to a differential equation of order two. Those equations can be very hard to solve.

Let's try to find a way to hide this complication. We can define the Lagrangian as:

Here we can see the dependence of the Lagrangian with the generalized coordinates and the time. One of the components is the first derivative of a generalized coordinates. The Hamiltonian will substitute this second parameter by a generalized momenta:

How can we do that? With the Legendre transformation. I will not demonstrate it, but basically, with the following formula, we can do this substitution:

So, I've to calculate the Lagrangian to get the Hamiltonian. And then what? How do I get my equation of the movement of my system? If we use the total differential of the Hamiltonian as defined in the previous equations, with the help of the generalized momenta definition, we quickly reach to the Hamilton equations which are:

Ok, fine. I've another way to calculate the same equations. Has it some meaning? It's that the unique advantage? Yes, it has a physical meaning, and no, it has more advantages. 

If we have a system with scleronomic constraints (without time dependence), the Hamiltonian represents the total energy. And in this cases, the Lagrangian is called the free energy. The demonstration is quite easy starting from the Legendre transformation.
The differences to use the Newton's, Lagrange's or Hamilton's mechanics to solve a problem are mainly the problem itself. For a quite easy problem, use the Newton's mechanics; you won't have to calculate the energies neither differential equations. For more complexe problems, you can use both Lagrange's or Hamilton's mechanics, it will depends on the number of variables, on their relation, on the differential equation resulting of the Lagrange equations.

This can best be shown in an exercise.

Classical Mechanics - Hamiltonian

Sir William Rowan Hamilton (1805-1865) was the creator of the quaternions, but also known for its contributions in the Newtonian mechanics (as he reformulated it in the Hamiltonian mechanics) and in the Quantum mechanics.

Why do we need another reformulation of the Newtonian mechanics having the Lagrangian? Let's examine the Lagrangian:

As we can see, the Lagrangian depends on the kinetic energy, which has the velocity as its component. The velocity is a derivative of the position. And in the first term of the Lagrange's equation, the Lagrangian is derived by the time, this means that we'll have the position derived twice by the time, which lead to a differential equation of order two. Those equations can be very hard to solve.

Let's try to find a way to hide this complication. We can define the Lagrangian as:

Here we can see the dependence of the Lagrangian with the generalized coordinates and the time. One of the components is the first derivative of a generalized coordinates. The Hamiltonian will substitute this second parameter by a generalized momenta:

How can we do that? With the Legendre transformation. I will not demonstrate it, but basically, with the following formula, we can do this substitution:

So, I've to calculate the Lagrangian to get the Hamiltonian. And then what? How do I get my equation of the movement of my system? If we use the total differential of the Hamiltonian as defined in the previous equations, with the help of the generalized momenta definition, we quickly reach to the Hamilton equations which are:

Ok, fine. I've another way to calculate the same equations. Has it some meaning? It's that the unique advantage? Yes, it has a physical meaning, and no, it has more advantages. 

If we have a system with scleronomic constraints (without time dependence), the Hamiltonian represents the total energy. And in this cases, the Lagrangian is called the free energy. The demonstration is quite easy starting from the Legendre transformation.
The differences to use the Newton's, Lagrange's or Hamilton's mechanics to solve a problem are mainly the problem itself. For a quite easy problem, use the Newton's mechanics; you won't have to calculate the energies neither differential equations. For more complexe problems, you can use both Lagrange's or Hamilton's mechanics, it will depends on the number of variables, on their relation, on the differential equation resulting of the Lagrange equations.

This can best be shown in an exercise.

Classical Mechanic - Hamiltonian exercise

Let's try to solve the pendulum equation with the Newton's, Lagrange's and Hamilton's mechanics.

Newton's Mechanics

The K vector shows the direction of the movement of the pendulum. It can be defined as |K| = mgsinα. Consider the displacement of the mass at the end of the pendulum as x. So the vector K remains as:

We know the value of the displacement x and its second derivative as:

If we substitute those values in the precedent equation, and making the approximation of the sinus for small displacements of we get:

Solving this differential equation of order 2, we get:

Lagrange's Mechanics

Here, we must first find the kinetic and potential energies:

With those energies, we can obtain the Lagrangian:

Now we can apply the Lagrange's equation to obtain the motion of the pendulum:

This is the same differential equation as the one get with the Newtonian mechanics.

Hamilton's Mechanics

We start from the Lagrangian, and the generalized momentum:

Now, with the value of the generalized momentum, we can substitute the derivative of α from the Lagrangian and get the Hamiltonian:

If, now, we apply the Hamilton's equations:

Substituting the values of the generalized momentum, we reach to the same differential equation as in the two other cases; with the same final result.

Conclusion

As you've see, the three methods hopefully gave the same result, which confirm that they are a reformulation of the same mechanics. The Newton's mechanics is more simplistic, and for problems with more constraints, you must deal with a system of several equations.

The Lagrangian's mechanics reduce the number of equations to the number of constraints. This is the method with less equations to solve, but you must deal with almost a differential equation of order two.

And the Hamiltonian's mechanics have twice the number of equations than the Lagrangian, but you with easier calculus, as the Hamilton equations does have second degree derivatives.

Classical Mechanics - Lagrangian

Joseph-Louis Lagrange (1736-1813) was a mathematician, physicist and astronomer which made important contributions to analysis, number theory and classical and celestial mechanics. Mécanique analytique (1788) was his treatise where he first introduced the analytical mechanics. He first invented the Lagrangian function which verify the Lagrange equations. The Lagrangian is a reformulation of the classical mechanics, which simplify the calculations.

But before going directly to the Lagrange equations, let's start with the virtual displacement. Consider a system made of a pipe which rotate on a fixed at one end, and where some particles come from the fixed end of the pipe and get out from the pipe by the other end. The real displacement of the particles will be the rotating displacement plus the centrifugal force. This displacement, is commonly denoted as dr. The virtual displacement is the displacement if all the forces and constraints acting on the system do not change. This is, if for an infinitesimal amount of time, the pipe will not rotate. Then, the particle will only have the centrifugal force, which made only the radius vector. This displacement is commonly denoted as δr.

Let's now return to the Lagrange equations. The second law of Newton says that the force on a particle is:

If we decompose the force into the applied force F_a, and the constraints force f, the Newton's law becomes:

Considering a system in equilibrium, the total work of the system will be zero. As the work is the force multiplied by the displacement, the virtual work will be also zero:

In the case of a rigid body, the multiplication of a contraint force of a single particle of the rigid body with its virtual displacement will be zero; as the virtual displacement will be perpendicular to the constraint force. Imagine a particle on a pendulum, the contraint force will from the particle to the fixed point of the string, and the virtual displacement will be tangent to the circle made by the rotating string. This leads the previous equation to the principle of virtual work:

We also know that the force is the derivative of the momentum:

Substituting this on the principle of virtual work, we have the D'Alembert principle:

The D'Alembert principle states the dynamic equilibrium of a system of particle.

Let's now consider a holonomic contraint r_i(q₁, q₂, ..., q_N, t) = 0. A holonomic constraint is all the equations which restrict the movement of our particles system where the time is involved in those equations. This means that each coordinate r_i can be defined by some equations where generalized coordinates q_i are defined.
Then we can define the velocity as:

And the virtual displacement as:

Note that the time does not appear here, since the virtual displacement, by definition, considers only displacements of the coordinates. Going back again to our equation of the virtual work, we can use generalized coordinates:

Here, Q_k is called the generalized force as it depends on the generalized coordinates. Note that q does not necessarily have the dimension of force as Q does not necessarily have the dimension of force, but the product of both must have the dimension of work (it might be the torque for Q and the angle for q).

Let's go back to the D'Alembert principle and use the generalized coordinates for the momentum:

Consider now the following relation:

For the last term, we can interchange the differentiation variable to obtain the velocity:

Substituting this result in the previous equation:

From the above equation obtained of the velocity, we know that this equality is true:

Substituting all this, we get:

Reordering this equation:

In the previous equation, we can now see the term of the kinetic energy T:

Making the adequate substitutions in the D'Alembert principle with the generalized coordinates:

Let's now use a potential function. Consider the forces are derivable from a scalar potential function V as follows:

By definition of the generalized force, we can link the potential function as follows:

Which lead to the final equation:

I've also included V in the first term of the equation, which does not affect the result as the potential field does not depend on the generalized velocities. This lead to the Lagrange's equation with the substitution of L = T - V which is known as the Lagrangian.

But what's the Lagrangian and the Lagrange's equation for? From the values of the kinetic and the potential energies, we can easily get the equation of movement of a system of particles. With the Lagrange's equation we'll have a system of equations (one per generalized coordinate) which is only composed by the kinetic and potential energy (which are quite easily to obtain in most of the cases).

To see this, let's solve an exercice.