Sir William Rowan Hamilton (1805-1865) was the creator of the quaternions, but also known for its contributions in the Newtonian mechanics (as he reformulated it in the Hamiltonian mechanics) and in the Quantum mechanics.
Why do we need another reformulation of the Newtonian mechanics having the Lagrangian? Let's examine the Lagrangian:
As we can see, the Lagrangian depends on the kinetic energy, which has the velocity as its component. The velocity is a derivative of the position. And in the first term of the Lagrange's equation, the Lagrangian is derived by the time, this means that we'll have the position derived twice by the time, which lead to a differential equation of order two. Those equations can be very hard to solve.
Let's try to find a way to hide this complication. We can define the Lagrangian as:
Here we can see the dependence of the Lagrangian with the generalized coordinates and the time. One of the components is the first derivative of a generalized coordinates. The Hamiltonian will substitute this second parameter by a generalized momenta:
How can we do that? With the Legendre transformation. I will not demonstrate it, but basically, with the following formula, we can do this substitution:
Why do we need another reformulation of the Newtonian mechanics having the Lagrangian? Let's examine the Lagrangian:
As we can see, the Lagrangian depends on the kinetic energy, which has the velocity as its component. The velocity is a derivative of the position. And in the first term of the Lagrange's equation, the Lagrangian is derived by the time, this means that we'll have the position derived twice by the time, which lead to a differential equation of order two. Those equations can be very hard to solve.
Let's try to find a way to hide this complication. We can define the Lagrangian as:
Here we can see the dependence of the Lagrangian with the generalized coordinates and the time. One of the components is the first derivative of a generalized coordinates. The Hamiltonian will substitute this second parameter by a generalized momenta:
How can we do that? With the Legendre transformation. I will not demonstrate it, but basically, with the following formula, we can do this substitution:
So, I've to calculate the Lagrangian to get the Hamiltonian. And then what? How do I get my equation of the movement of my system? If we use the total differential of the Hamiltonian as defined in the previous equations, with the help of the generalized momenta definition, we quickly reach to the Hamilton equations which are:
Ok, fine. I've another way to calculate the same equations. Has it some meaning? It's that the unique advantage? Yes, it has a physical meaning, and no, it has more advantages.
If we have a system with scleronomic constraints (without time dependence), the Hamiltonian represents the total energy. And in this cases, the Lagrangian is called the free energy. The demonstration is quite easy starting from the Legendre transformation.
The differences to use the Newton's, Lagrange's or Hamilton's mechanics to solve a problem are mainly the problem itself. For a quite easy problem, use the Newton's mechanics; you won't have to calculate the energies neither differential equations. For more complexe problems, you can use both Lagrange's or Hamilton's mechanics, it will depends on the number of variables, on their relation, on the differential equation resulting of the Lagrange equations.
The differences to use the Newton's, Lagrange's or Hamilton's mechanics to solve a problem are mainly the problem itself. For a quite easy problem, use the Newton's mechanics; you won't have to calculate the energies neither differential equations. For more complexe problems, you can use both Lagrange's or Hamilton's mechanics, it will depends on the number of variables, on their relation, on the differential equation resulting of the Lagrange equations.
This can best be shown in an exercise.

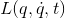

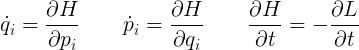
While this explanation is remarkably coherent, I still have a problem understanding "time" as a discrete value separated from positions coordinated in space. Time IS movement as movement IS change, but there are "levels" of energy which also change quantitatively, perhaps as heat generates expansion or potential energy induces kinetic energy where Newton presents points of equilibrium between forces, not positions in proportion to "time." So these equations imply the existence of instantaneous "times" in a field or a cross-ratio of (q,p) determining such a position; how did "time" combine both its instantaneous moment and its generalized nature?
ReplyDeleteThese relations in three variables don't produce a scalar value in series at the "same time" they present a vector force for differentiation. The difference refers you back to the rational difference between distance and time in the concept of Velocity (via Newton), so these positions where actions and reactions take place are also skewed toward radical values in plane geometry rather than real values in solid space.
The science is quantitative, especially as you assumed this primary value for Velocity. The difference should be between rest and movement, not progress or inertia, where that quantity reflects a coordinated action in three quantities.
First of all, the separation of the time as a independent variable for the Hamiltonian is that the time is not a variable which affects the constraints of a physical system. Both q and p are variables which defines the contraints of the system. For scleronomic systems (where the system does not depend on the time) the variable "time" will not appear in the Hamiltonian.
DeleteNow, being in a configuration space (with generalized coordinates and not Cartesian coordinates) we take into account the virtual displacement of the system, which could not be equals to the actual motion of the system.
The science is quantitative, yes, but in there, the values migrates from some physical values as the velocity, to some other more abstract as the generalized coordinates.