When you have an equation as F(x, y) = 0, this is an implicit solution of the equation. Sometimes you can solve this equation for y, but only if the function satisfy the implicit theorem (https://en.wikipedia.org/wiki/Implicit_function_theorem). If the equation does satisfy the conditions of the theorem, you can solve it as y = f(x).
How to do that with Maxima? First, we will use the function solve() to obtain all the solutions of the given equation. The solve() function will give you all the available solutions if there are, or none if it can't. Then we use the output of solve() as input for sublis().
What does sublis()? It substitute a list of given values into a given equation. When we get the solutions with solve() we do the substitutions of the solutions by y.
Let's see an example:
Here we defined f as an equation. With solve() we solve the equation f for y. In this example we only have a single solution, but solve() will give us all the existing solutions in a list. And finally, we give the output of solve() to sublis() to get y solved.
The previous example is too easy. Let's make a generic function which leads with multiple solutions given by solve().
Here we iterate with a for loop over all the solutions given by solve(), and at each step, we append a new y solution to our list which will be returned as our output.
This procedure can only be used if the function f satisfies the implicit theorem. Otherwise, we must solve the equation with numerical procedures.
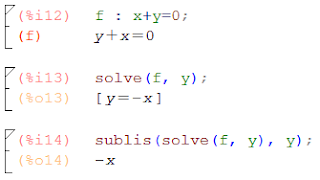

No comments:
Post a Comment