Maxima - Loops & Conditions

Here, I'll explain two very important tools used in every programming language. The loops and conditions. When you're creating an application, the way you want the application to be executed is not always linear, but you'll want your application to go one way if... or another way if... You also could want to perform a single manipulation a repeated amount of times. Let's see some examples:

I think the code is easy to understand. The main statements here, are if, then and else. With if you specify the condition, you can specify an equality (=), a comparison (>=, >, <, <=) or an inequality (!=). With then you start the statements you want to execute if the if-condition is satisfied, you can add as many as you want. And finally, the else statement define the code which will be executed if the if-condition is not satisfied. Let's continue with a more complicated example:

As you can see, the if-condition can have multiple conditions, separated with and or or as logical operators.

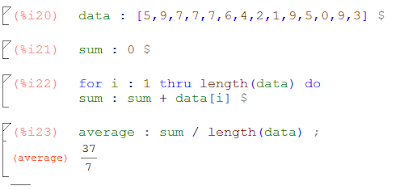
The for loops. When you want to run a task a determined amount of times, you can use the for loops. Those loops are build with three parts: an initial part where you specify the variable which will behave as the index, and its initial value; the final condition until when the loop must be executed; and the steps the index must be incremented at each loop. Let's do an example: give the average of the elements in a list (this can be done directly with another instruction, but that's not what we want to test today):

In some cases, you could want to have another for loop inside the first for loop, but this must done with caution, as the execution time increase exponentially. If you have three for loops, and the elements to handle are 10 or 12, your code will be executed 1000 or 1728 times (a difference of 728 just adding two elements to the original list).
There are some variants of the for loop, you can specify an iteration from an initial value to a final value (with thru); a condition which must be satisfied to iterate the loop (with while); or a condition which must not be satisfied to iterate the loop (with unless).

Let's continue with a simple exercise:

Write an application which gives the Taylor series of a function for a grade from 1 to n.

To solve this problem, we can just do a for loop, and make the Taylor series of the function from 1 to n, but if n is high, this could cost a lot of execution time. Let's examine the Taylor series: it's the consecutive derived of a function. So if we do manually the derived from 1 to n, we have at each loop step a new solution. Let's see the code:

Our function is called taylor_grade_n with the inputs: the function, the points where to get the Taylor series, and the grade. We start by saving the function in an temporal variable to avoid modify the input value. Then we stock the first value (the function without any derived) in a list, which we will append the rest of the values in the for loop. At each step of the for loop, we append the previous value of the result list with the new derived multiplied by (1/index!)*(x - x0).